17 juni - snedfördelat och olika testresultat samt inlägg från en användare

 Hej, sommaren är här och jag tar sommarlov fram till någon gång i augusti med bloggandet. Fortsätt skicka frågor ändå, så svarar jag vid tillfälle och bloggar om det i höst.

Jättekul när ni svarar på mina blogginlägg, läs längst ned om Roberts inlägg om centrala gränsvärdessatsen, så som han tänker runt det.

Om du vill lära dig mer om val av test, hur man kollar normalfördelning så kan jag varmt rekommendera Statistikakademins introduktionskurs SPSS 1: (se länk). Ja kommer bara snudda lite vid sånt som tas upp under kursen nedan, träning ger färdighet och man lär sig ju mer statistik man gör. 

Data-materialet

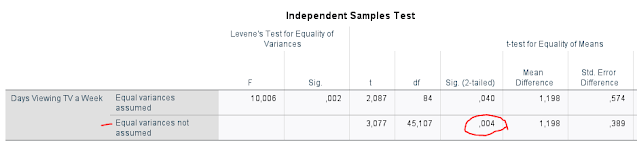
Först tänkte jag visa hur om datat såg normalfördelat ut och sen tänkte jag testa 2 grupper och visa hur olika resultat det blir om jag väljer vanligt t-test jämfört med ickeparametriska alternativet 

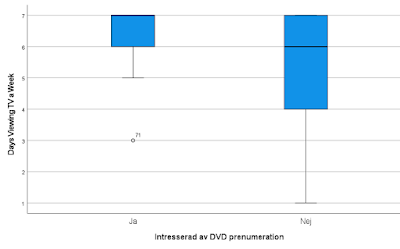
Så här ser variablerna ut som jag ska testa mot varandra, antal dagar i veckan som varje person kollade TV och gruppvariabeln buyfona: om de är intresserade att köpa en film-prenumeration.

Det är inte många personer i ja-gruppen (ja: 16, nej:70).

Normalfördelat eller snedfördelat?

Först kollar jag om det är normalfördelat med kommandot "Explore" (Analyze - Descriptive Statistics)

I plots-knappen brukar jag lägga till "normality tests" och "histogram".

Jag brukar först ta en titt på histogrammen och boxplottarna, och tycker det ser snett ut i båda grupperna.

Histogrammet på nej-gruppen visar snedfördelning tydligt, de flesta kollar TV 7 dagar i veckan 

Kollar jag i boxplotten så kan jag få en bra bild av båda grupperna och ser att medianen i JA-gruppen är 7 dagar och medianen i NEJ-gruppen är 6 dagar. Den individ nr 71 som ligger i Ja,gruppen kommer dra ner medelvärdet kommer ni se längre ned.

Kollar jag den beskrivning som också kommer ut så ser jag att medelvärde och median tycks skilja dig en del i JA-gruppen (se de 2 övre blå ringarna). 

Just när det är så få som 16 personer så är det känsligt när det är snedfördelat och medelvärdet och medianen skiljer sig åt. Vi pratade förra veckan om centrala gränsvärdessatsen där man på många håll ser att har man över 30 personer blir det inte lika känsligt (se även Roberts inlägg längre ned).

Om skewnessvärdet (röda) är minst dubbelt så stor som den siffran bredvid (std error) så kan det också tyda på snedfördelning.

Grupp tester som visar OLIKA resultat

Då kommer det känsliga och det är om jag väljer olämpligt test så blir grupperna signifikant skilda ifrån varandra och om jag väljer ett mer stabilt ickeparametriskt test blir de inte signifikant skilda. 

Det olämpliga testet är t-test, den bygger på medelvärden och eftersom medelvärdet och medianen skilde sig i den lilla gruppen med 16 personer så kommer det påverka resultatet. Medelvärdet drogs ner av en person till 6 och det kommer resultera i en signifikant skillnad mellan JA - och NEJ-gruppen. P-värdet är bara 0.004!

Om vi kollar det ickeparametriska testet Mann Whitney U, så blir det ickesignifikanta skillnader mellan JA och NEJ-gruppen (p-värdet är 0.071)

Så jag säger att det nedre testet är korrekt att använda när man har så få som 16 personer och det är så snedfördelat så medelvärden och t-test är olämpligt.

Men om de nu varit fler än 30 personer (eller 40 som jag också sett som gränsvärde), hade det blivit mer stabilt då och hade det varit ok att använda t-test trots allt? Det här vågar jag inte svara på, men enligt centrala gränsvärdessatsen så kan man tydligen tolka att det är OK att köra t-test. Men i ärlighetens namn skulle jag inte våga. 

Som jag brukar säga på kursen SPSS 1 (Statistikakademin: det är aldrig fel att ta ickeparametriskt test om man är osäker)

Se Roberts inlägg hur han resonerar:

Jag läste detta om CGS och normalfördelningen, en viktig fråga som många stöter på. Tumregeln om minst 30 är ju ett helt korrekt svar på hur många observationer som behövs för att ett medelvärde ska uppföra sig någorlunda i linje med en normalfördelning. Den frågan kan vara viktig. Men samtidigt är det kanske en annan fråga som styr om man ska överge t-test till förmån för någon icke-parametrisk metod, jag tänker mig något i stil med ”Klarar de t-fördelningsbaserade metoderna av så små stickprov som jag råkar ha?”. Och där har det visat sig att de metoderna ändå är förhållandevis robusta. Det fick jag inte lära mig själv i grundutbildningen på stenåldern, utan det dök upp i en kursbok som jag använde på LTU för rätt länge sedan, Basic Practice of Statistics av David Moore.

 Bild 1 : ur kursboken

Bild 2 ur kursboken: 

De bifogade bilderna är hämtade från den boken, och bild 2 är kanske särskilt relevant. Där hävdas att det i t-test för två stickprov och med små stickprov, typ högst 15, krävs att man kan använda normalfördelningen för att beskriva variablerna. Med fler räcker det att variablerna är någorlunda symmetriskt fördelade. Med någorlunda stora stickprov kan man skotta in nästan vad som helst, t-testet pallar med avvikelser från normalfördelningsmönstret. Det har rimligen delvis med CGS att göra, men är ändå inte riktigt samma sak.

 

Det finns referenser också, de Moore hänvisade till är

 

1)      Posten, H., The robustness of the two-sample t-test over the Pearson system, Journal of Statistical Computation and Simulation, 6(1978), pp. 295-311

 

2)      Posten, H. et al, Robustness of the two-sample t-test under violations of the homogeneity assumption”, Communications in Statistics, 11 (1982) pp. 109-126.

 

En liten detalj kring detta med att testa fördelningsantaganden. Med små stickprov kan man så gott som aldrig påvisa avvikelser från (ex) normalfördelningen. Och riktigt stora material kommer aldrig att vara i linje med normalfördelningen, och det är väl rätt rimligt. Att verkliga mätningar skulle uppföra sig som en matematisk funktion är rätt orimligt. Men om frågan är om man kan använda t-test för att jämföra två populationsgenomsnitt så är det alltså kanske inte så himla viktigt att veta om normalfördelningen passar eller inte?

-- Slut på Roberts inlägg --